L’équation d’onde

Attention : article assez dense en maths, sur un sujet que j’ai découvert en l’écrivant. Il pourrait donc y avoir des erreurs. N’hésitez pas à commenter si quelque chose vous semble bizarre !

L'

autre jour, je regardais ma guitare et je me suis rendu compte que je ne savais pas comment les ondes se comportent sur une corde, d’un point de vue mathématique. Comment se propagent-elles ? La corde est fixée entre deux points. On la pince en la déplaçant à un certain endroit, puis on la lâche. Que se passe-t-il alors ?

Dérivation

Imaginez une corde avec une tension $T$ et une masse linéique (ou densité linéaire de masse) $\mu$. On va s’intéresser uniquement aux déplacements verticaux de la corde, qu’on supposera petits (comme sur un instrument à cordes). On va modéliser notre corde par une fonction $y$, qui donne le déplacement vertical en fonction de la coordonnée $x$ et du temps $t$.

Oublions le temps un instant, et regardons une situation statique. Voici un petit bout de corde avec la tension qui s’exerce à ses deux extrémités.

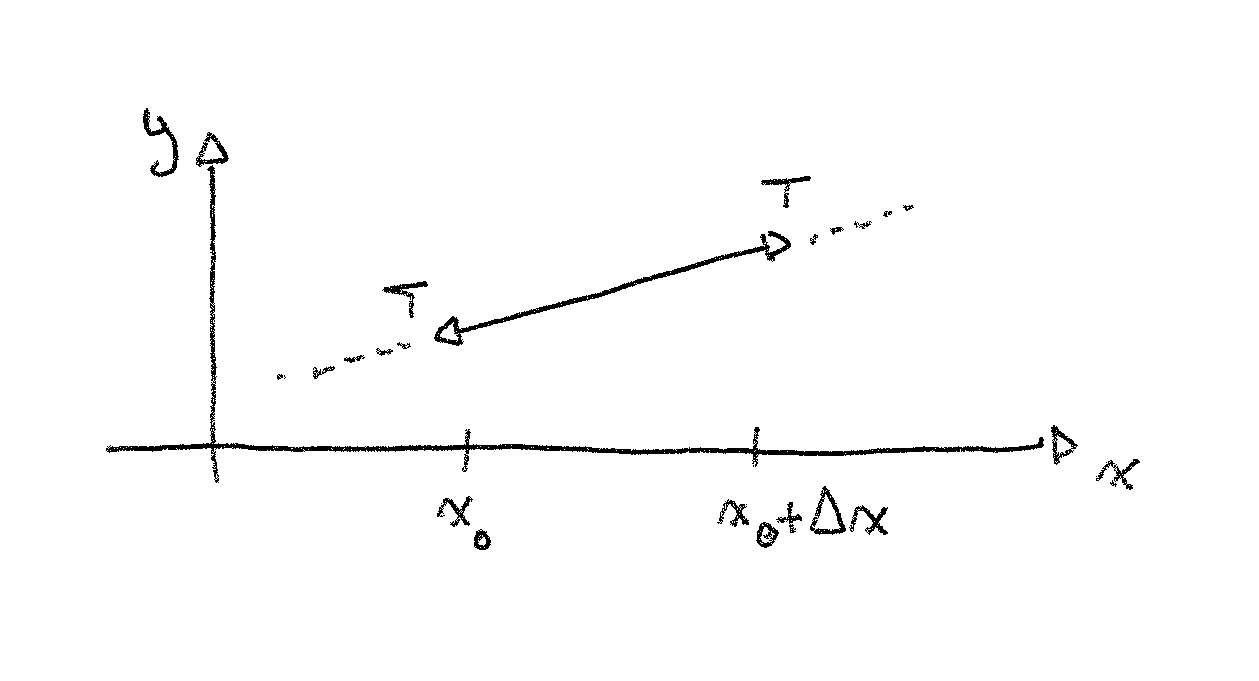Il ne se passe pas grand-chose ici : la corde est droite, les forces de tension s’équilibrent, tout reste en place. Mais regardons ce qui se passe quand il y a une courbure.

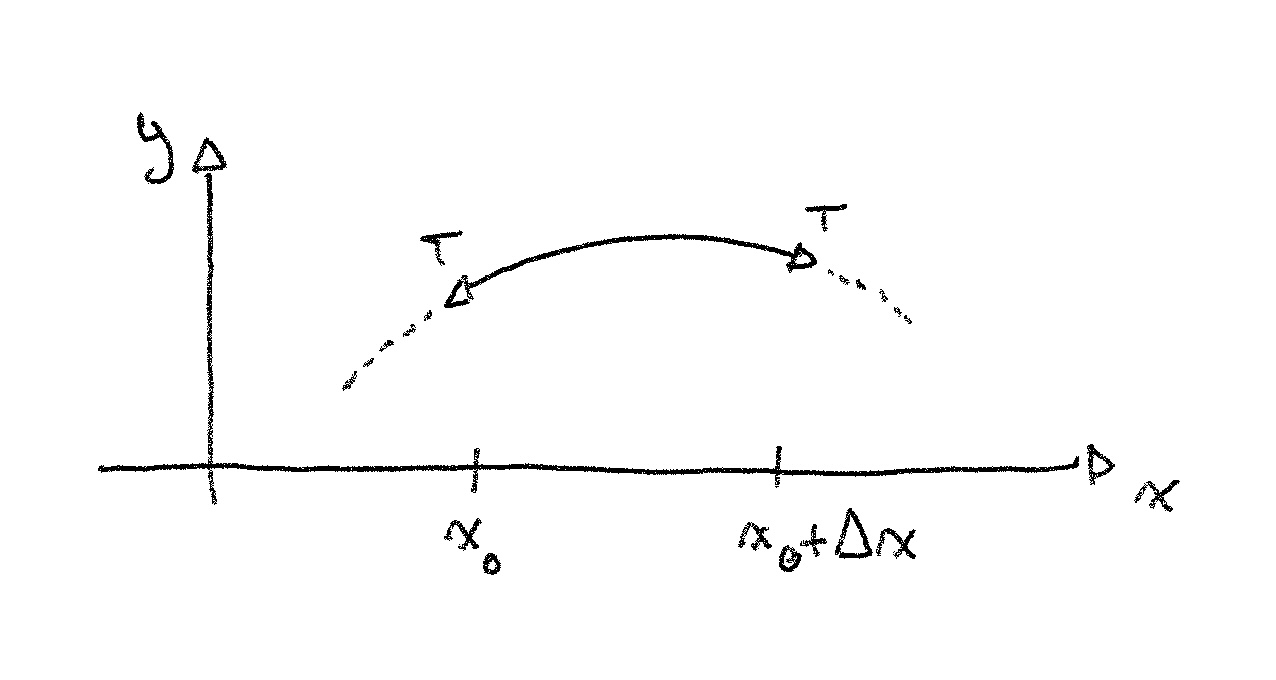Ici, on imagine bien que la force nette va tirer le bout de corde vers le bas. On peut trouver facilement la masse de ce segment : $m_{\Delta x} = \mu \Delta x$. Si on arrive à trouver la force nette qui s’applique dessus, on pourra utiliser la deuxième loi de Newton.

On a supposé que le mouvement de la corde se faisait uniquement selon l’axe $y$. Ça veut dire qu’on peut se concentrer sur les forces verticales agissant sur notre segment, en $x_0$ et $x_0 + \Delta x$.

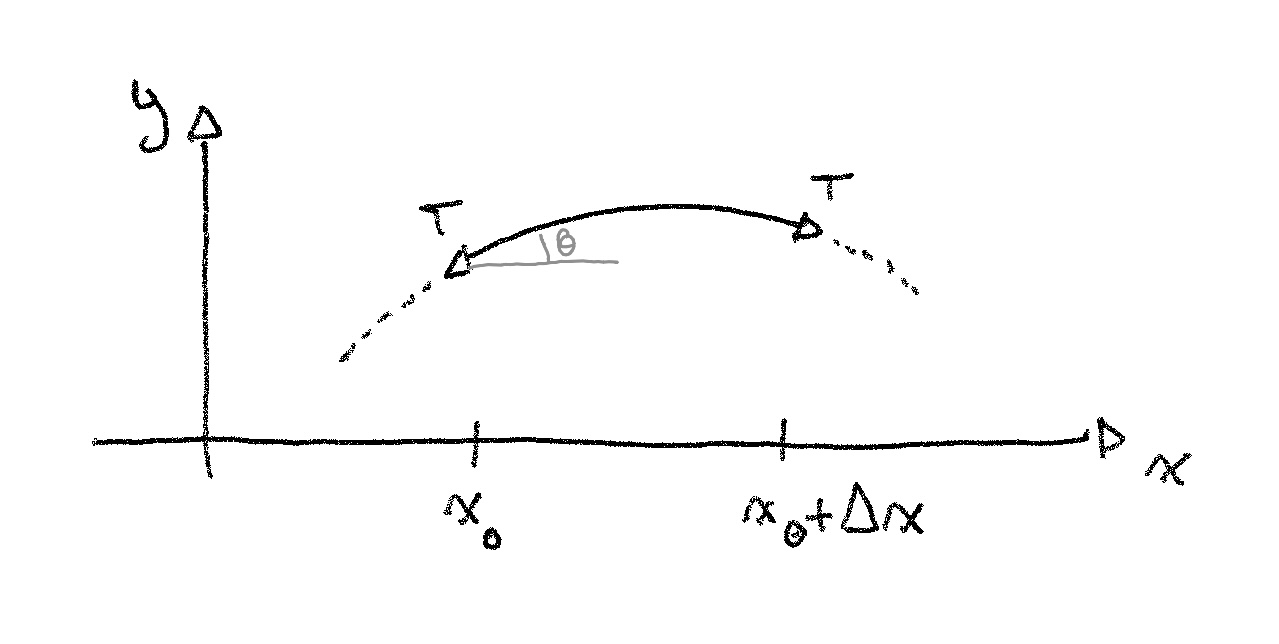
Sur ce schéma, on voit que la force verticale en $x_0$ est $F_{x_0} = -T \sin(\theta)$. Comme on a supposé les déplacements $y$ petits, on peut faire l’approximation des petits angles chère aux physiciens, et utiliser la pente plutôt que le $\sin$ ⁰, ce qui donne :

On peut trouver la force à l’autre extrémité de la même manière ¹:

On peut les additionner pour obtenir la force nette agissant sur ce petit bout de corde.

Parfait ! On a tout ce qu’il faut pour appliquer la deuxième loi de Newton. Réintroduisons aussi le temps dans l’équation.

En réorganisant un peu :

En supposant que notre fonction $y$ est suffisamment régulière (‘well-behaved’), on a :

Au final, en prenant un $x$ général au lieu de $x_0$, notre équation devient :

Ou, comme on la présente plus souvent :

Ça correspond bien à notre intuition de départ : plus la corde est courbée à un endroit, plus elle va bouger vite. Plus la tension est élevée, plus ça va vite ; plus la masse linéique est grande, plus c’est lent. Le ‘sanity check’ est passé.

À partir de là, maintenant qu’on a cette équation aux dérivées partielles, on peut faire deux choses : s’arrêter ici et aller simuler ça sur un ordinateur, ou essayer de trouver des solutions explicites.

Solutions

Bien sûr, cette équation est idéalisée, elle ne reflète pas toute la réalité. Par exemple, il n’y a pas d’amortissement, un mouvement continuerait indéfiniment. Mais elle est quand même utile pour comprendre comment les ondes se propagent dans ce milieu, surtout si on peut trouver la forme générale des solutions.

Séparation des variables

Essayons de simplifier le problème en ‘testant’ l’hypothèse que $y$ peut s’écrire comme le produit de deux fonctions plus simples, chacune dépendant d’un seul paramètre :

Ça simplifie énormément le problème et limite les formes que $y$ peut prendre. Substituons $y$ par ce produit dans l’équation d’onde :

Quand $X(x) \neq 0$ et $T(t) \neq 0$, on peut réarranger un peu ²

Chaque côté ne dépend que d’une seule variable, ce qui signifie qu’ils sont tous les deux égaux à la même constante !

Résolution de chaque côté

Prenons d’abord le côté gauche

Si on cherche une fonction dont la dérivée seconde est quasiment la même (à un facteur près), on pense à l’exponentielle. Posons $T(t) = e^{at}$. On obtient :

Si $\alpha > 0$, on a $T(t) = e^{\sqrt{\alpha} t}$, mais on ne cherche probablement pas une fonction exponentielle, car elle ne satisfera pas nos conditions aux limites. Par contre, si $\alpha < 0$, on a $T(t) = e^{\pm it\sqrt{-\alpha}}$, ce qui ressemble beaucoup plus aux ondes dont on parle depuis le début.

C’est logique intuitivement : si $T''(t)/T(t) > 0$, la fonction a une courbure positive quand elle est déjà positive, ce qui la fait croître encore plus. Dans l’autre cas, elle a une courbure négative, ce qui rappelle la force de rappel qu’on a trouvée dans la première partie.

Pour simplifier, posons $\alpha = -k^2$, de sorte qu’on ait :

On peut suivre exactement la même procédure pour $X$, qui obéit à la même équation avec une constante multiplicative en plus.

et essayer $X(x) = e^{b x}$

Donc $b = \pm ik \sqrt{\frac \mu T}$ . Définissons $\lambda = k \sqrt \frac \mu T$ pour simplifier.

Nos deux solutions ‘élémentaires’ résultantes (en fait quatre, si on compte les signes) sont :

Mais l’équation est linéaire, ce qui signifie que n’importe quelle combinaison linéaire de ces solutions est aussi une solution. La forme générale est donc :

Où $A_1, A_2, B_1, B_2 \in \mathbb C$

Application des conditions aux limites

Spatiales

On est prêt à appliquer quelques conditions aux limites. D’abord, la corde est fixe en $x=0$ et $x=L$, ce qui signifie que $\forall t$ on a $y(0,t) = y(L,t) = 0$. La première condition se traduit par :

Donc au moins un des membres est nul. Si le terme de droite était nul, ça signifierait $A_2 = B_2 = 0$, ce qui mène à une corde immobile. Sinon, on doit avoir $B_1 = -A_1$, et

En appliquant la condition à l’autre bout de la corde, on obtient :

Ce qui est valide pour tout $n \in \mathbb N^*$, signifiant que $X$ peut être une superposition de ces solutions :

Temporelles

Si on pense au mouvement d’une corde de guitare, au moment où on la pince initialement, sa vitesse est nulle partout (avant que le musicien ne la lâche). Ce qui signifie que $T'(0) = 0$ :

On peut maintenant simplifier l’écriture de $T$ :

On sait aussi que $k=\lambda \sqrt \frac T \mu = \frac{n\pi} L \sqrt \frac T \mu$, ce qui veut dire qu’on a aussi une superposition ici :

Solution finale

En combinant ces termes, avec de nouvelles constantes $a_n$, on a ⁴

Et en utilisant la formule $\sin(a)\cos(b) = \frac 1 2 (\sin(a+b) + \sin(a-b))$ on obtient

C’est une forme plus facile à interpréter : pour chaque fréquence (mode $n$), il y a une onde qui va vers la droite et une autre vers la gauche. Sous cette forme, on voit aussi que $c = \sqrt \frac T \mu$ est la vitesse à laquelle l’onde se propage. Réécrivons-le avec cette simplification :

En fait, il nous reste une inconnue, ou plutôt une infinité : tous les coefficients $a_n$. Mais on peut les déterminer à partir de l’état initial de la corde $y(x, 0)$. Si on injecte $t=0$, on obtient :

Ce qui n’est autre que la décomposition en série de Fourier de l’état initial.

(TODO ajouter une explication sur les séries de Fourier)

Pour en savoir plus

Simulation

Allez, un peu de fun. En discrétisant le domaine (spatial et temporel), on peut modéliser la corde au temps $t$ par un tableau $\tilde{y}_t \in \mathbb R^n$, où $n = L / \Delta x$ et $\Delta x$ est le pas spatial. On peut suivre la vitesse verticale de la corde en chaque point avec un autre tableau $\tilde{v}_t \in \mathbb R^n$.

De cette façon, on connaît l’état du système au temps $t$, et on peut le mettre à jour en se basant sur l’équation d’onde. On fait ça en utilisant une approximation par différences finies de la dérivée seconde spatiale (qui est juste l’approximation qu’on obtient en considérant la définition de la dérivée) :

À partir de ça, en utilisant l’équation d’onde, on obtient une approximation $\tilde{a}(x,t)$ de l’accélération. Intégrer une fois est facile à approximer :

Ceci nous donne la variation de vitesse, avec laquelle on peut mettre à jour notre $\tilde{v}_{t+\Delta t} \leftarrow \tilde{v}_t + \Delta \tilde{v}$ et en ‘intégrant’ à nouveau…

…on obtient la mise à jour de notre $y$ en faisant $\tilde{y}_{t+1} \leftarrow \tilde{y}_t + \Delta \tilde{y}_t$ et le cycle recommence, approximant la nouvelle position et la nouvelle vitesse à chaque pas de temps. Bien sûr, tout ça ne sert à rien si on ne peut pas le voir en action !

Comparaison avec une vraie corde